Howdy, Stranger!
It looks like you're new here. If you want to get involved, click one of these buttons!
Quick Links
Determine minimum width in a polygon with holes
Hi there. I have a single polygon with holes. I need to somehow determine the minimum width along the entire polygon. I assume this should be an easy task, but given the points of a polygon are generated at the corners, I have no way to iterate through points on the sides.
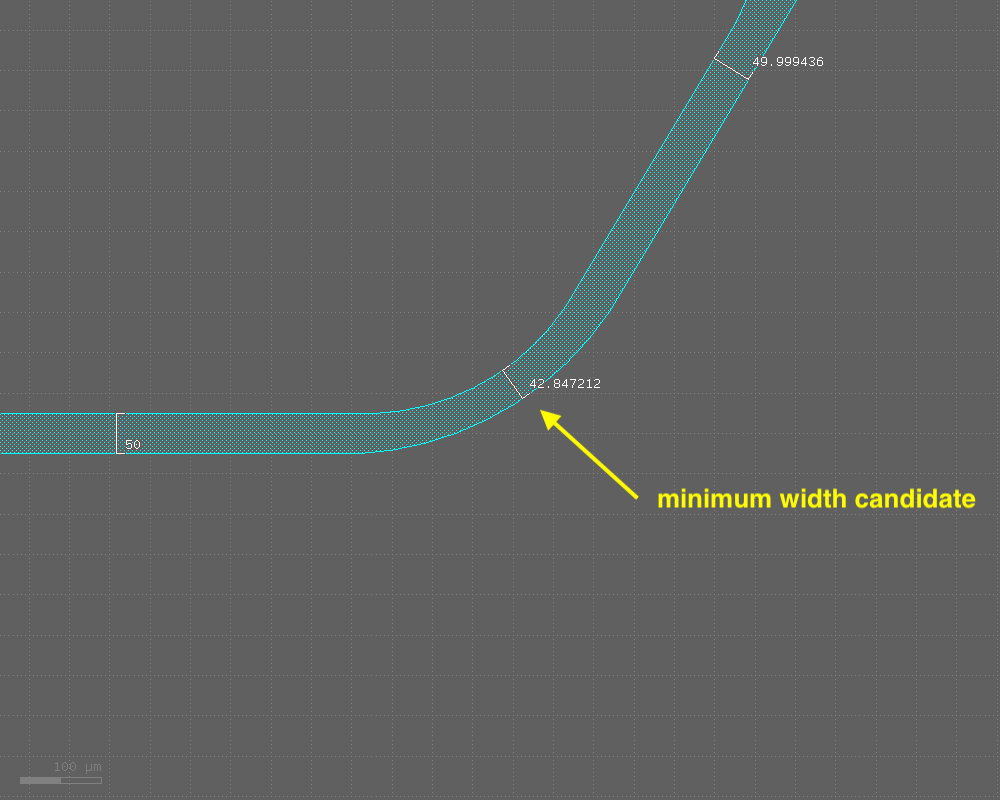
Here is an image of what I am trying to accomplish via Python script:
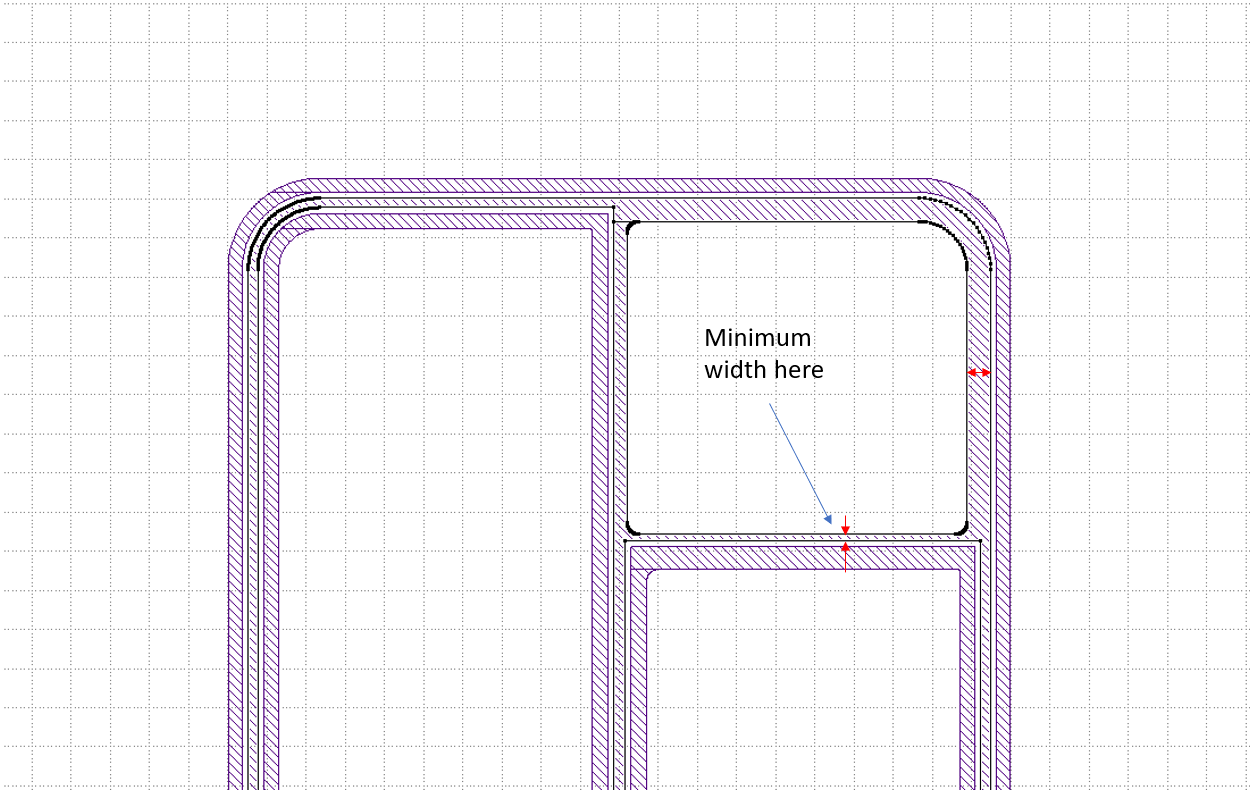
I want to write a function that takes in this layer/region and returns the minimum width of the polygon.
Thank you ahead of time for any help.
Comments
Hi,
To me, this problem seems to be not an easy task :-(
Several years ago, I wrote a KLayout Python script that estimates the minimum and maximum width of a polygon without holes. In my case, the polygon was like a very long Path with varying (at random) widths. Therefore, it was impossible to visually find out where there are the minimum and maximum width candidates.
My basic idea was to repeat the negative resizing by increasing and adjusting its amount until the original single polygon breaks into several polygons. In other words, repeat the negative resizing until the first disconnection occurs, where the number of polygons becomes from one to N > 1.
Once I find the locations where the original polygon breaks up, I can use the ruler (measure) tool to obtain a more accurate minimum width.
Suppose I continue the negative resizing after finding out the first disconnection. In that case, I will finally reach the moment when all polygons are on the verge of disappearing (N -> 0), which suggests nearly the maximum width.
Like the case of minimum width, I can use the ruler (measure) tool to get a more accurate maximum width at the location.
Now let me apply the above-said algorithm to a case with holes.
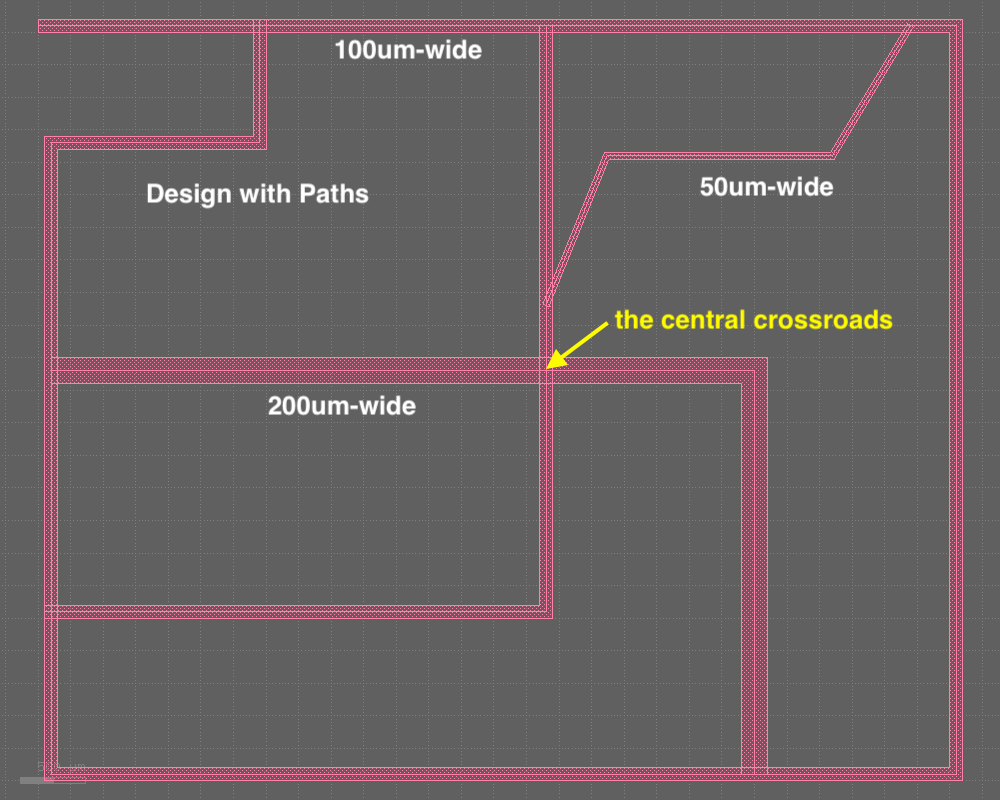
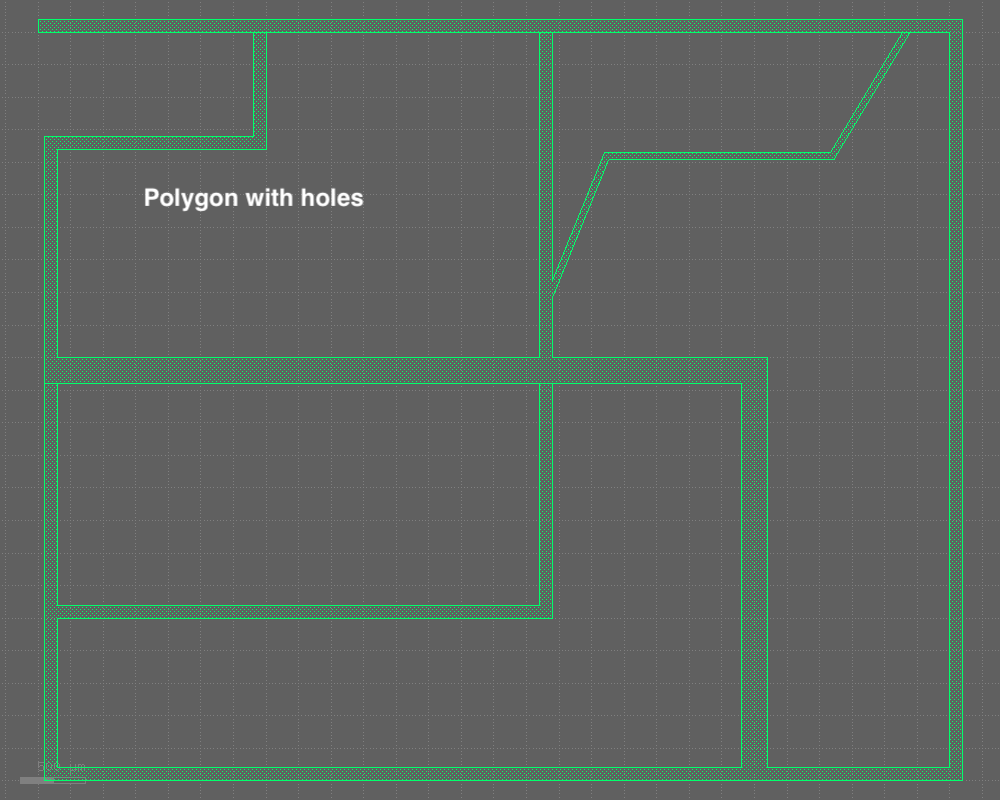
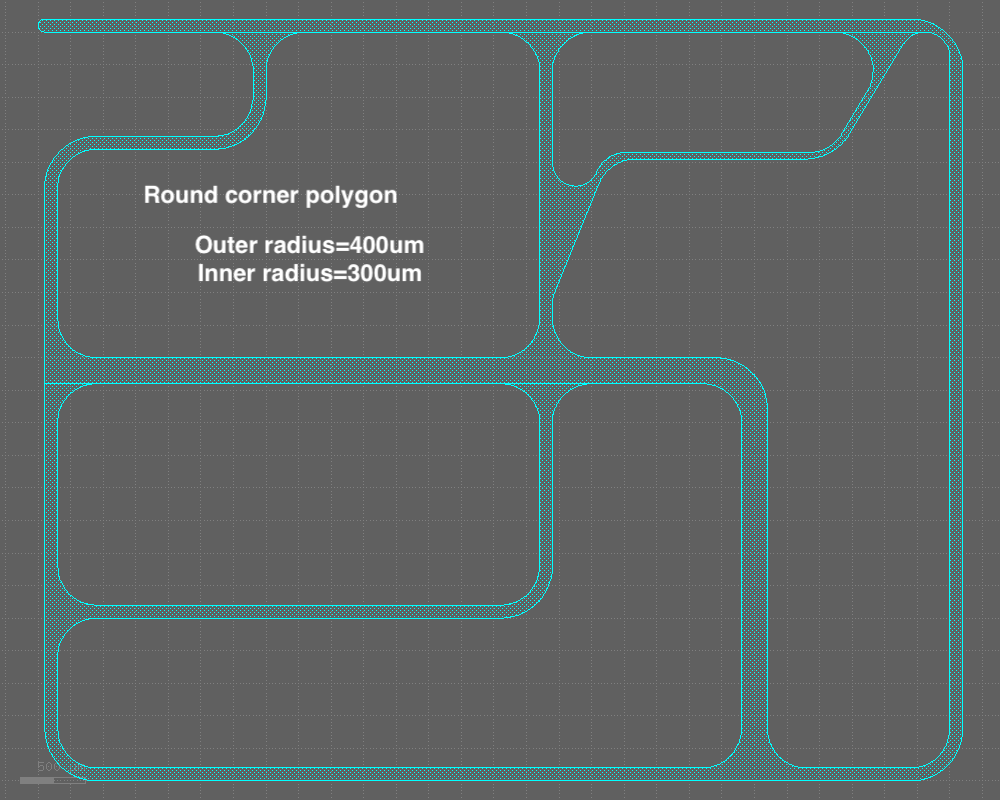
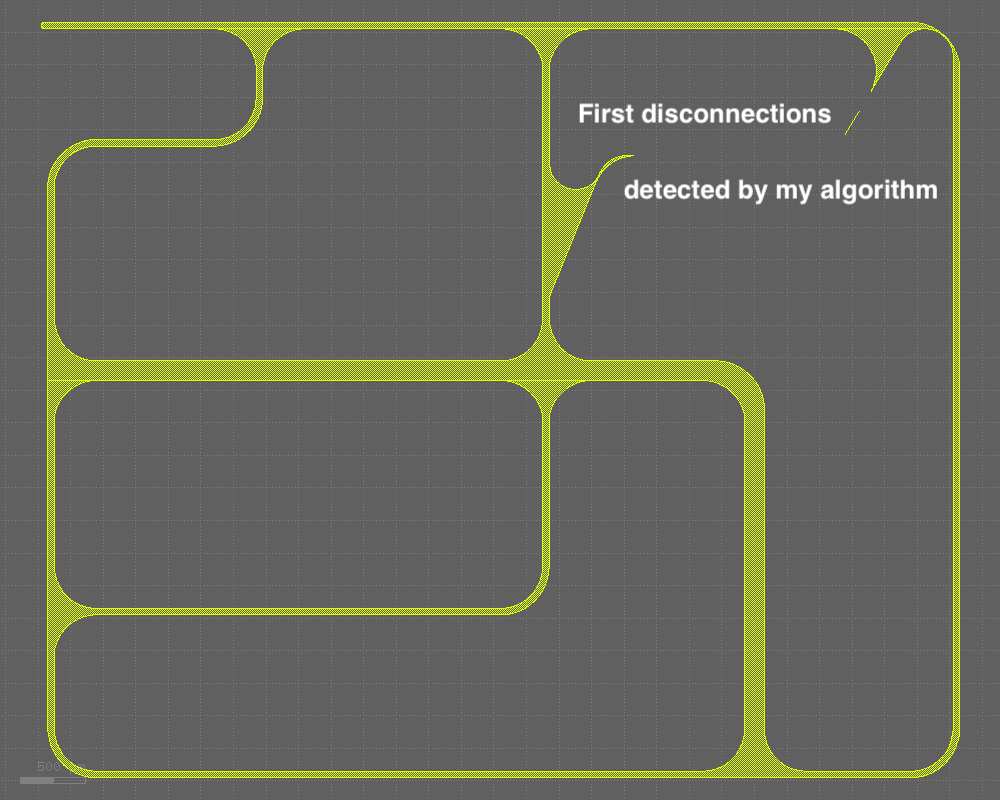

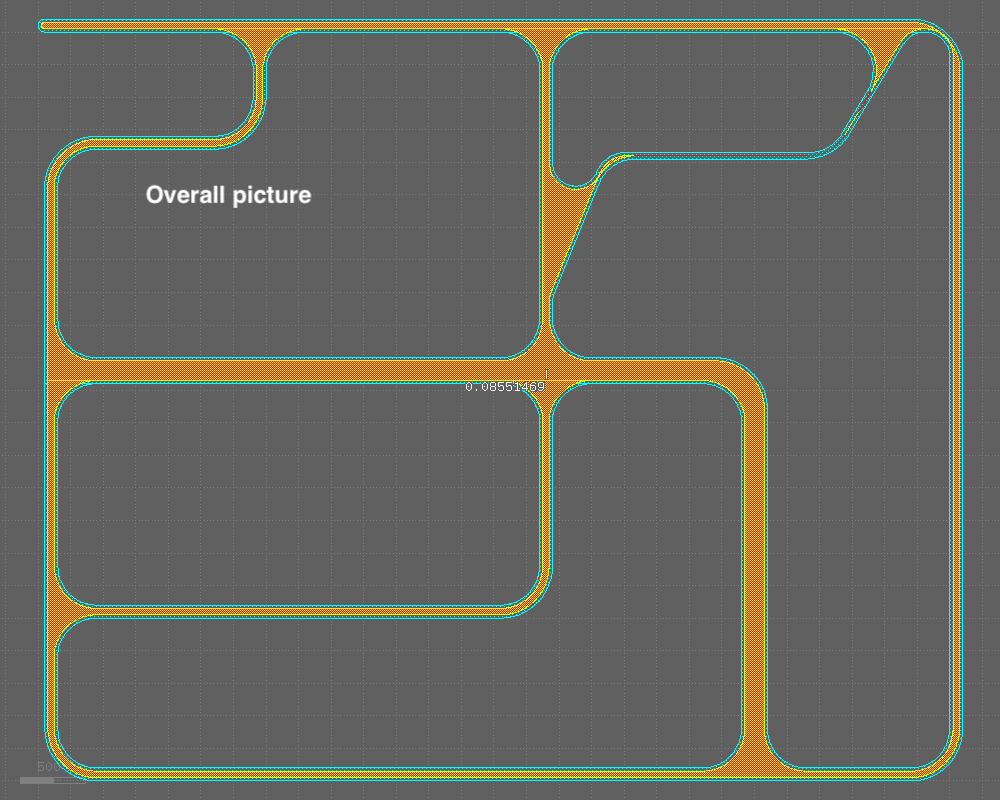
Please refer to the images attached below.
At a glance, they look OK. However, the minimum width is not correctly estimated.
The reason is that due to the presence of holes, N=1 remains unchanged after the actual first disconnection occurred (see the image below).
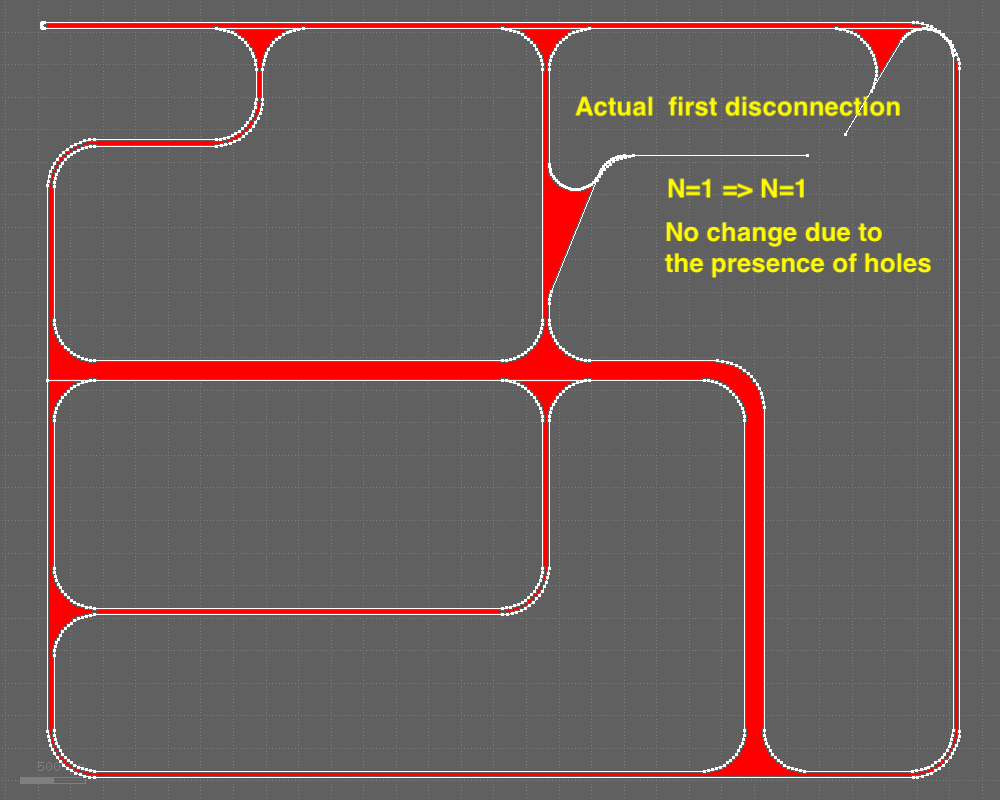
Q: Does the algorithm work perfectly if a polygon generally has no holes?
A: No, it doesn't, unfortunately. I have already encountered such a case. The algorithm works preferably so far to solve my problem.
It is apparent that we need a more elaborated algorithm to handle a polygon with holes.
@kazzz Thanks for another masterpiece of well-documented thoughts!
Here are my thoughts: I recently published a small script that works on the principle of applying a sizing and using bisection to find the minimum space (https://www.klayout.de/forum/discussion/2299/bisection-of-drc-checks-to-find-min-distance#latest).
It runs on the whole layout or rather the current cell or a specific layer. If you replace "space" by "width" you should be able to find the minimum width.
Is that helpful?
Matthias
@Matthias,
Thanks a lot for sharing the idea. Yes, it is helpful, as shown below.